[경영자를 위한 AI와 딥러닝] 중간고사 공부

[경영자를 위한 AI와 딥러닝] 중간고사 공부]

2주차

• 신경망

• 구조

  • 700 ~ 1000억(100 BN)개 정도의 신경망 세포들
  • 신경망 세포들 간의 연결 고리
    • Dendrite
    • Axon: 신경세포의 몸체 (soma)
      • 포텐셜을 측정 (voltage) ; 포텐셜의 변화밖에 없음
        • spiking
        • bursting
        • chattering (갈수록 freq 빨라짐)
    • Synapse: 신경세포 간의 연결 (한쪽은 dendrite 한쪽은 axon)
      • neuro transmitter가 이동
      • electric potential을 통해 이동
      • 불확실성이 많은 확률적 프로세스; non-linear
      • connectionism; 연결주의; 모든 정보는 연결에 포함되어있다
    • Neural Computation
      • add/ subtract
      • multiplication
      • modification

• Neural Computation을 구현하는 것이 Deep Learning

  • 인공신경망 Artificial Neural Networks
    • Supervised Learning
    • Universal Function Approximator; 비선형적 관계까지 배울 수 있는 가능성
    • layered structures, deep
  • connectionism by alexander bain (2주차 강의 40분 쯤)
  • Neural Learning (Hebbian Learning Rule) 44분쯤

• Soma에 붙어있는 dendrit로 input

  • w as weight
  • axon을 통해 전달 (긴다리)
  • node가 역치를 기점으로 1 or 0 과 같은 signal 발생

  Perceptron

  • simplist neural network
  • computational model of mcculloch-pitts neuron

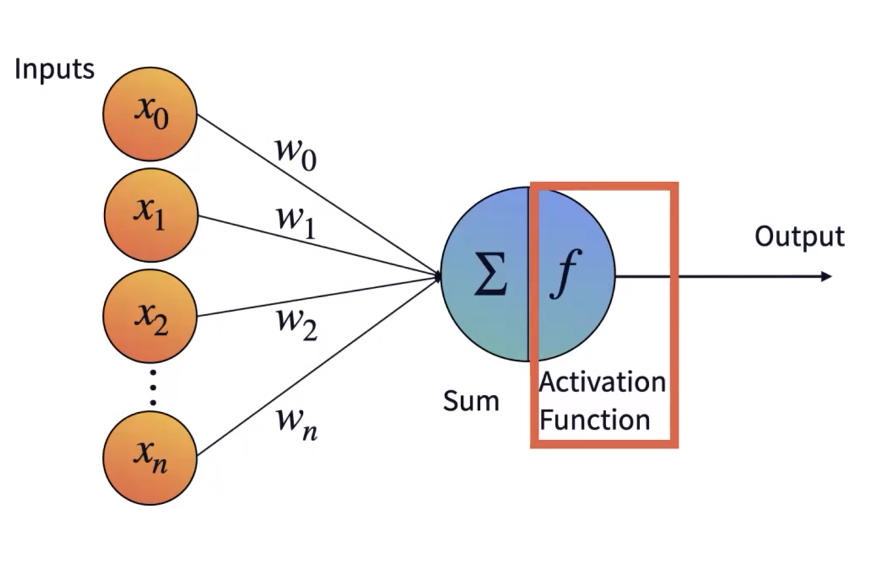
• activation function
  • step (계단)
  • sigmoid (S자)
• b as bias
  • eventually $y=f(w*x)$
• AND/ OR Gate
  • 
  • 
  • XOR Gate https://youtu.be/Fg00LN30Ezg?t=385
• Perceptron Learning Rule
  • 
  • a. initial learning model setting by setting w_i
  • b. pick random x and check if the current learning model is right
    • b-1. if $wx_1>0$, then do nothing, since it is right
    • b-2. if $wx_2<0$, then w<-w+$\epsilon$; bit change to model
  • c. keep going on until the end (satisfying all condition)
• Gradient Descent
  • 
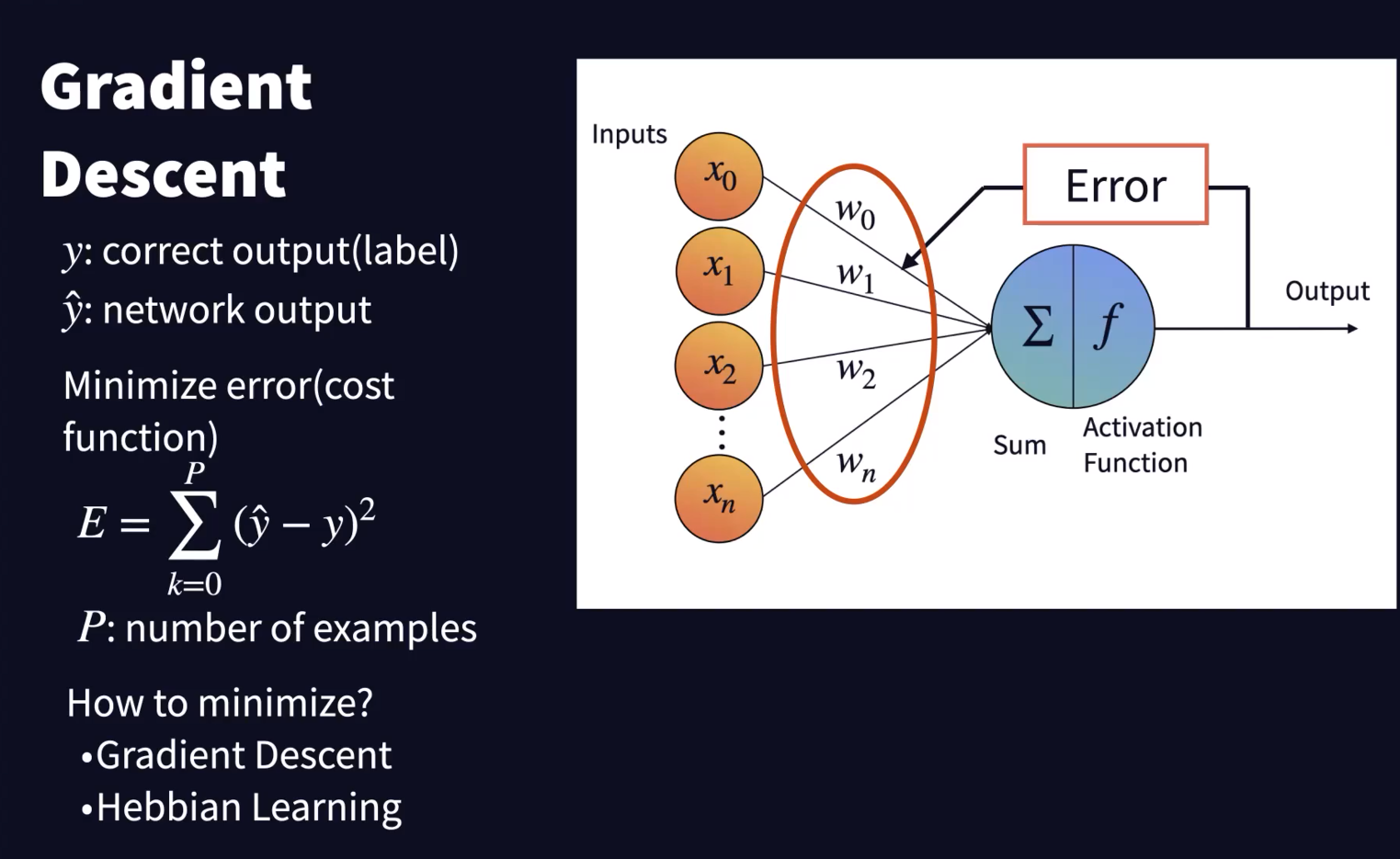
  • control the weight movement under the logistics of minimizing (mean-squared) error
• Summary
  • Perceptron is model for computation of a single neuron
  • Hebbian learning rule can be derived from gradient-descent of the cost function.

3주차

• Coding
• Hellow to Tensorflow, Keras

4주차

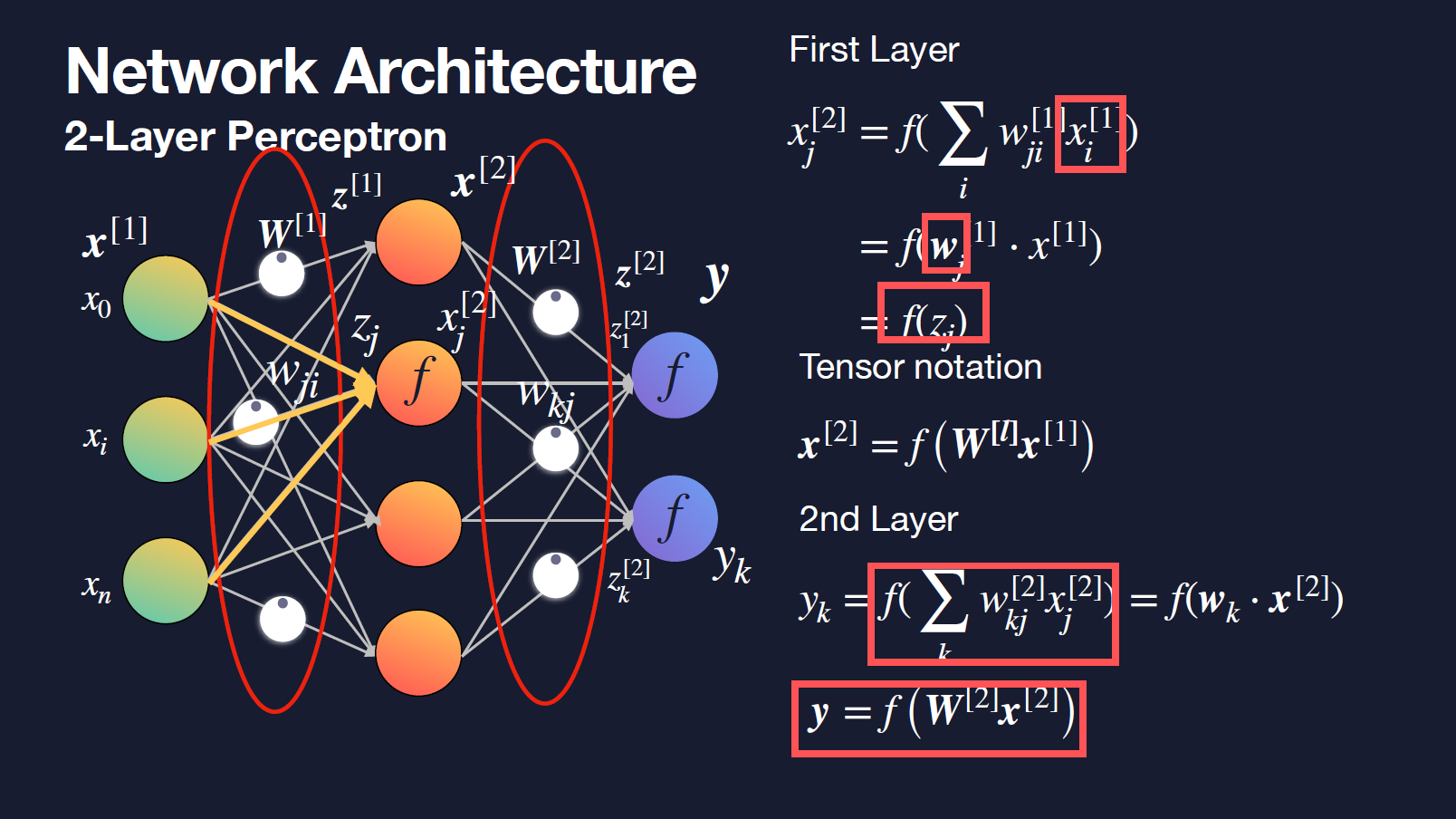
• Tensor Notation for Neural Networks

  • 
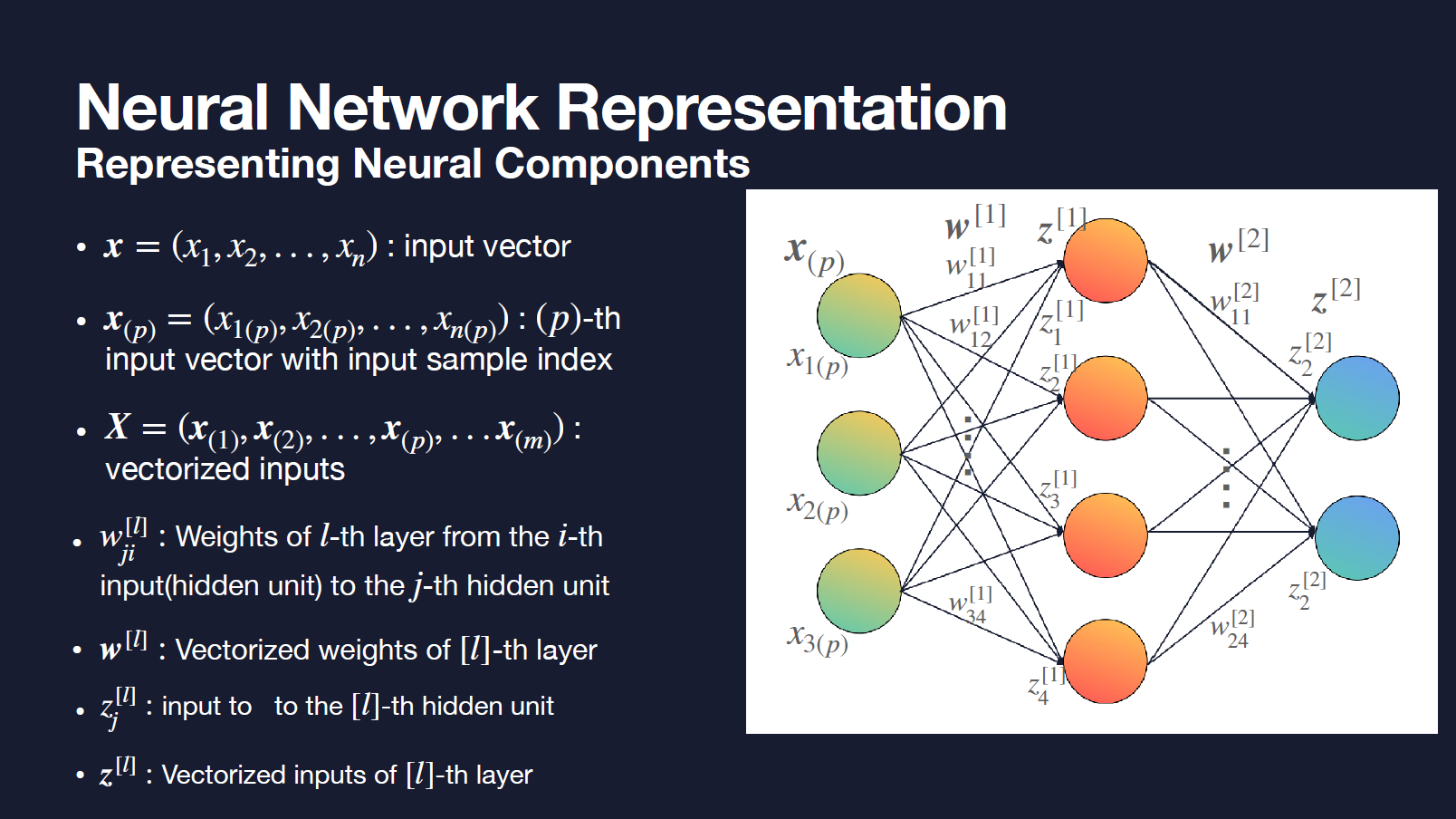
  • input as x
  • input vector as $x_{(p)}$
  • $X=(x_{(1)},x_{(2)},x_{(3)}, …)$ as vectorized inputs
  • $w_{ji}^{[l]}$ as weights of l-th layer from the i-th input to the j-th hidden unit
  • node의 개수는 사용자가 선택하는 것이 아님, 이것을 만들어나가는 과정 자체가 딥러닝
    • hidden layer, hidden node의 역할들 (구조들).. 블라블라
  • TensorFlow
    • Compute Tensors
    • automatically compute the gradient of any differentiable tensors
    • keras 라이브러리에 새로운 function이 contributed
    • Tensorflow는 cpu, gpu,tpu 등을 전방위로 활용하여 matrix calculation 등을 진행 (기반)
    • keras를 통해 텐서플로우 기반의 다양한 함수들 사용 가능

• Matrix Multiplication

  • 
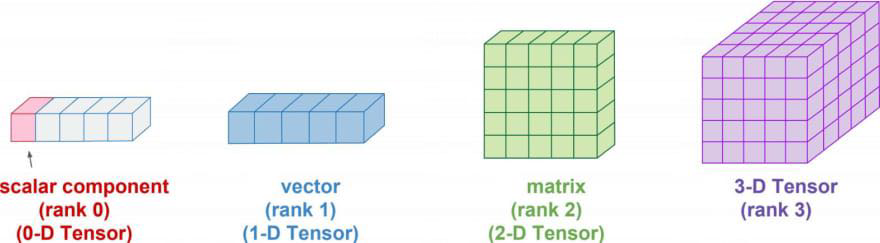
  • Scalar
    • rank 0 tensor (element of list(list is 1D; rank 1))
  • Vector
    • rank 1 tensor
  • Numpy is a commonly used package for mathematical computation of list.
  • Using Numpy we can compute vector and tensor effectively.

5주차

• Neural Network is Universal Function Approximator
• Understanding Tensor Representation for Deep Neural Networks
  • X is tensorzied input
• 퍼셉트론으로 손글씨 인식 - Colaboratory (google.com)

6주차

• 디지털플랫폼 정부
• Multilayer Perceptron
  • Training MLP using Back-propagation
  • History: PDP Group
    • Parallel Distributed Procesing
    • Paul Werbos’ Backpropgation Algorithm (역전파)
    • it’s all about adjusting weights
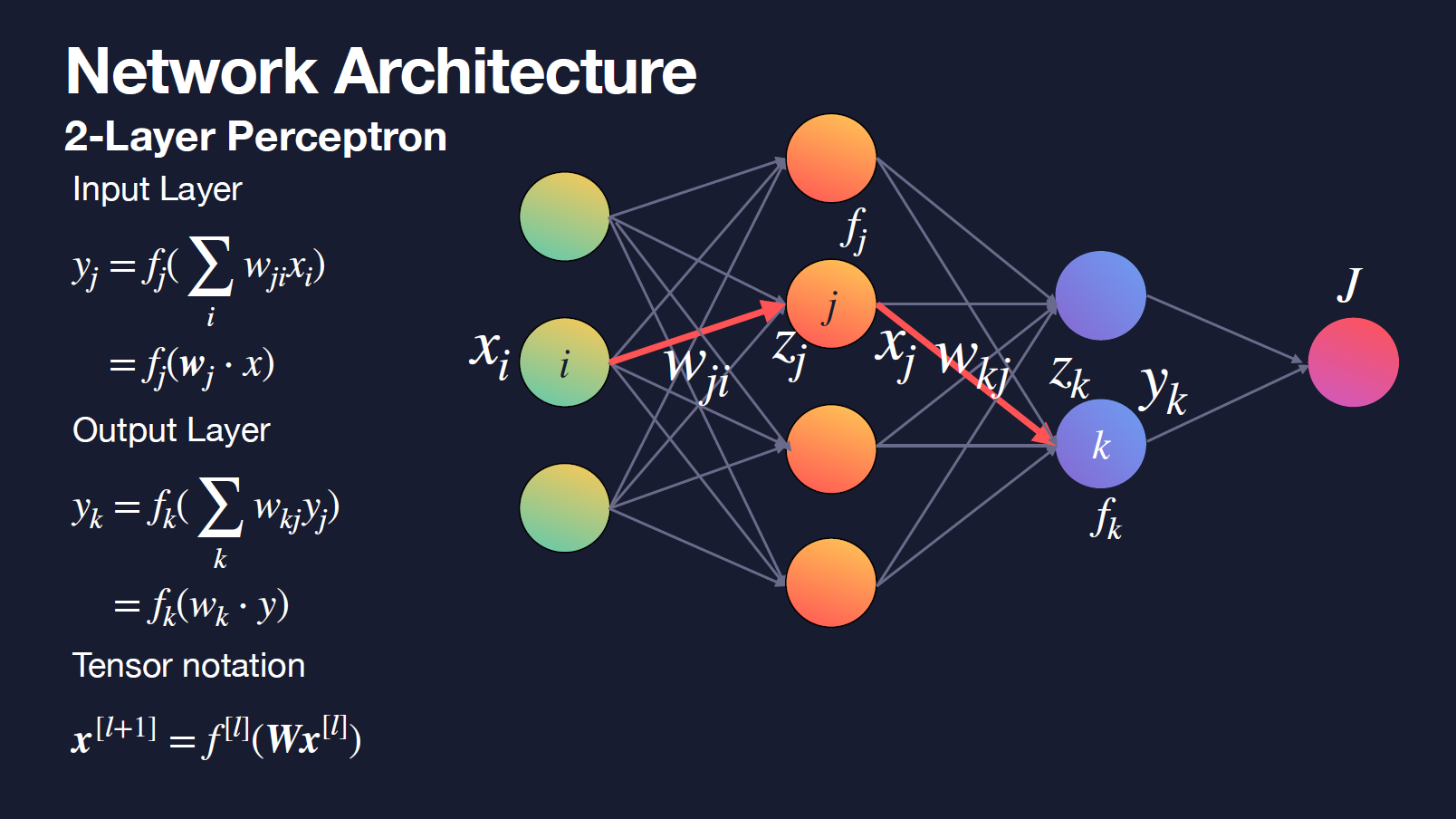
• Signals Propagate Forward
  • input이 weight를 통해 hidden node를 거쳐 output으로 가는 forwarding
  • Cost Function
    • 실제 정답과 model로부터의 결과 간의 차이
    • $J=(\hat\y-y)^2$
    • Chain Rule : g’(x)f’(x)
    • output node에 실제 정답(target output)을 기반으로 backpropagation을 통해 weight 조절
• 
  • always, it’s all about adjusting weight
  • partial derivative (편미분)
    • $w_{t+1} <- w_t -\gamma\Delta _wJ$
• 
  • layer 역순대로 미분 and so on
• 

7주차

• Maximize Performance
  • ML Workflow
    • Gathering Data
    • preprocess
    • research the model
    • train
    • evaluate and update the model
    • predict with satisfied model, otherwise? train again and again
  • train and test
  • hyperparameters: 알아서 다해요
    • control the learning process
      • topology and size of a neural network
      • algorithm hyperparameters: learning rate, dropout rate, batch size
  • 
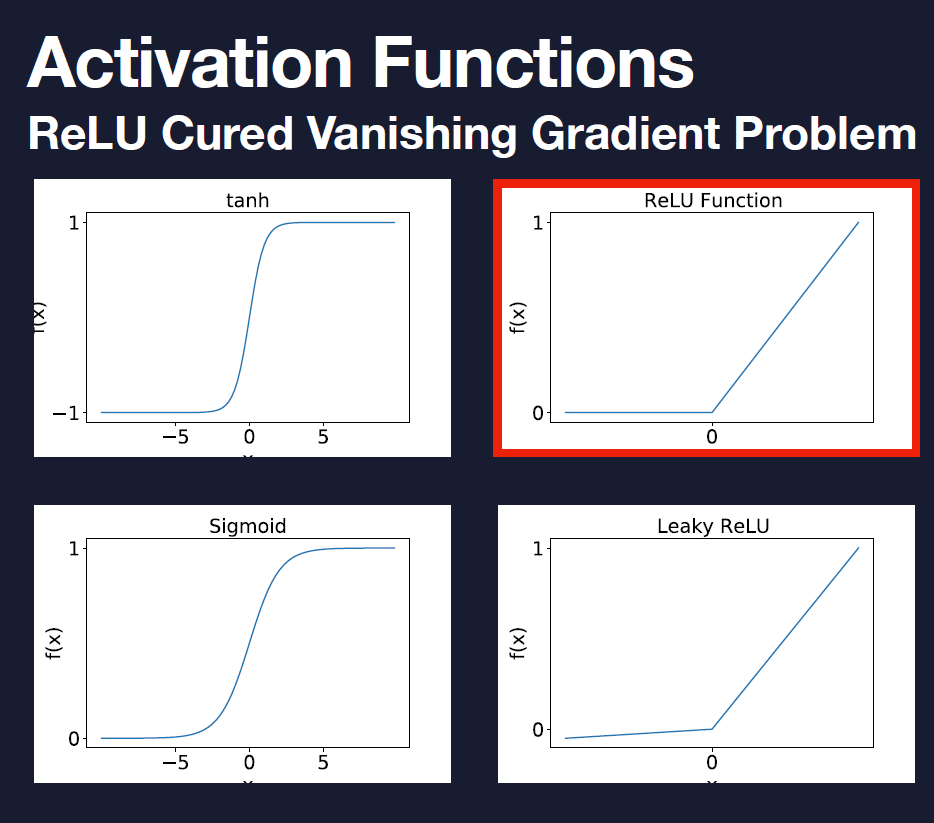
  • Why ReLU?
    • Sigmoid의 derivative 값이 작기 때문에 (대체로 .25 이하) 1보다 작은 값들을 계속 chain rule에 의해 곱하다보면 편미분값은 매우 작아지게 된다. 즉, vanishing
    • asymptotic behavior
    • ReLU는 derivative 값이 1 or 0뿐이므로 그 단점을 커버할 수 있음
• Various Implementatoin of Cost Function Optimization
  • Batch
    • loss function -> cost function을 minimize
    • gradient 계산량이 많고, 시간이 많이 걸림
  • Stochastic
    • each new gradient’s loss function
    • eventually approach to the optimal point
  • Mini-Batch
    • hybrid
    • sample examples
    • 두마리토끼, 계산량과 정확성
  • Choosing
    • small set<2000
      • batch gradient
    • large set
      • mini batch of size 64~512
• local minima
  • 쉬운게 없다
  • or plateau
  • multiple global minima
  • depends on cost function, the minima can be differed
• Learning Rate
  • parameters that control the learning process
  • $\gamma$
  • 
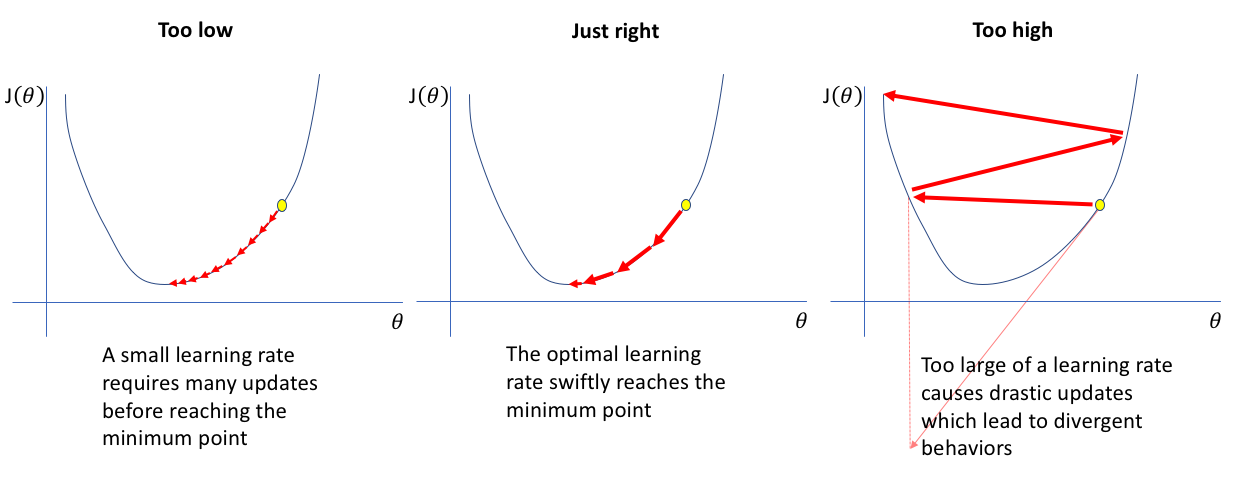
• Momentum
  • for finding global minima
  • 방향성에 대한 변수를 추가해 local minima에서만 머무르지 않도록
• Hyperparameter Tuning
  • Monte-Carlo Search
• Optimizers
  • Adam이 짱임 (최근으로선)
• Choice of Loss Function
  • mean squared error
    • regression or binary classification
  • cross entropy
    • multi class classification
    • paired with the softmax actiavtion function
• Under- and Over-fitting
  • fix underfitting
    • train longer
    • increase the model complexity
    • reducing regularizatoin
    • adding features to trainig data
    • different (appropriate) model or architecture
  • fix overfitting
    • adding more data
    • data augmentation
    • regularization
    • decrease model complexity
    • removing features from data
    • early stopping
      • balance between validatoin and error
  • what is regularization?
    • weight의 기울기를 급한 경사 안쪽으로
  • Preprocessing
    • normalization
    • data augmentatoin (데이터 증강 ex. 1->7개)
      • 
    • feature engineering
      • domain knowledge to extract features from raw data
      • applied ML
    • dimensionality reduction
      • Principal Component Analysis
      • Independent Component Analysis
      • Non-negative Matrix
      • Factorization
      • Uppropagation