[Econometrics] 9. Regression Discontinuity
#Sharp_RD #Fuzzy_RD #Validity_issue

술로 인한 불연속성
Regression Discontinuity
???: 결이 다르다
RD designs take advantage of the fact that, for some treatments, access to the treatment is a discontinuous function of one or more forcing variables.
RD comes in two styles, fuzzy and sharp.
Sharp Regression Discontinuity Design (SRD)
\[Y_i=(1-W_i)Y_{0i}+W_iY_{1i}\]여기서 W는 일종의 deterministic function이다. 이는 곧 아래와 같다.
\[W_i=1\{X_i\geq c\}\]c라는 기준을 전후로 W가 다른 값을 갖는 것이며, prob이 아래 그림처럼 c를 기준으로 0과 1로 극단적으로 나뉘는 것을 볼 수 있다.
(이 도식에서 세로축은 W이다.)
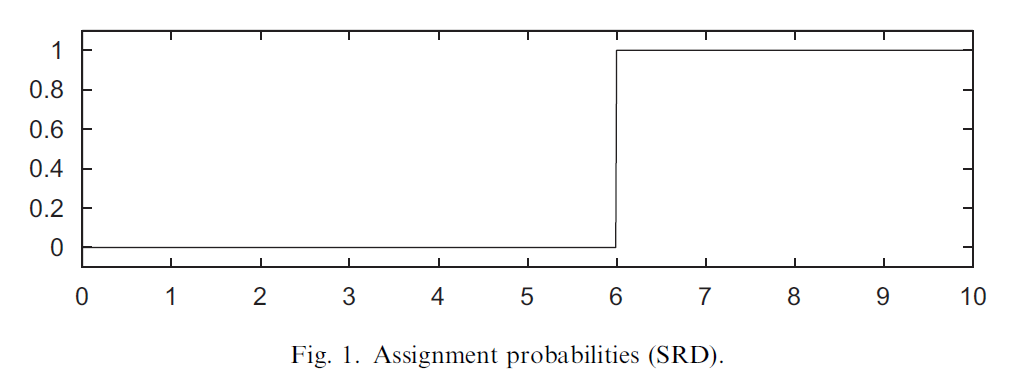
이때 가로축을 X, 세로축을 Y로 하는 도식화는 아래와 같을 것이다. 위의 점선은 $E[Y_1|X=x]$이고, 아래의 점선은 $E[Y_0|X=x]$이라고 볼 수 있다.
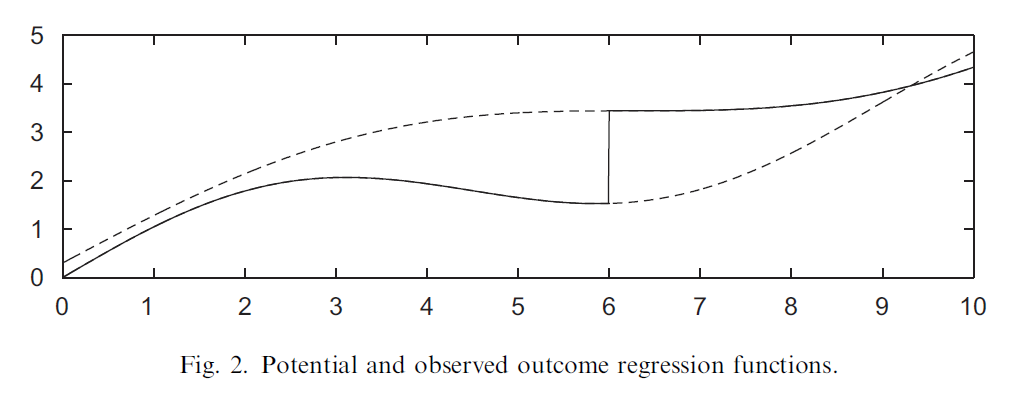
c 포인트로 서로 다른 방향으로 접근하는 극한값의 차이가 곧 treatment effect가 되는 것이라고 할 수 있다. RD에서의 treatment effect 변수를 지금부터 $\tau$로 칭하겠다.
\[\tau_{SRD}=E[Y_{1i}-Y-{0i}|X_i=c]\]Interpretation of $\tau_{SRD}$
$\tau$를 구하는데에 있어 두가지 조건이 필요하다. 1) Unconfoundness, and 2) Overlap Assumption이다.
\[\text{Unconfoundness Assumption (CIA): }\; Y_{0i}, Y_{1i}\perp\!\!\!\perp W_i|X_i\]W는 deterministic, 즉 randomness 자체가 없는 변수이기 때문에, 위 assumption을 만족하는데 무리가 없다.
문제는 overlap assumption에서 발생한다. 일반적인 overlap assumption은 아래와 같다. W의 특성 상 (위의 그림 참고) c를 기준으로 overlap assumption이 만족되지 않는다.
\[0<Pr(W_i=1 | X_i=x)<1\]overlap assumption에 대한 문제를 해결하기 위해 우리는 일종의 추정(extrapolate)이 필요하다.
Extrapolate
앞선 문제를 더 클리어하게 보여주는 수식은 아래와 같다.
\[\tau_{SRD}=E[Y_{1i}-Y_{0i}|X_i=c]=E[Y_{1i}|X_i=c]-E[Y_{0i}|X_i=c]\]마지막 전개에서 우측 항을 보면 c를 기점으로 모든 Y는 treatment를 받은 t=1 상태가 되기 때문에, $Y_{0i}$ 를 알 수 없다는 것이다.
하지만 극한을 사용한다며? 그 극한값을 구할 수 있기 위한 조건을 만족시켜야한다는 결론을 알 수 있다.
그 조건은 극한값을 향해가는 분포선(혹은 함수)이 연속이어야한다는 것이다. 우리는 이것을 Continuity of Conditional Expectation Functions Assumption 이라고 하겠다.
\[\displaylines{\text{Continuity of Conditional Expectation Functions Assumption}\\ E[Y_{0i}|X_i=x] \text{ and } E[Y_{1i}|X_i=x] \text{ are continuous in x}}\]Under this Assumption,
\[\tau_{SRD}=lim\;E[Y|c<-X]-lim\;E[Y|X->c]\]Fuzzy Regression Discontinuity Design (FRD)
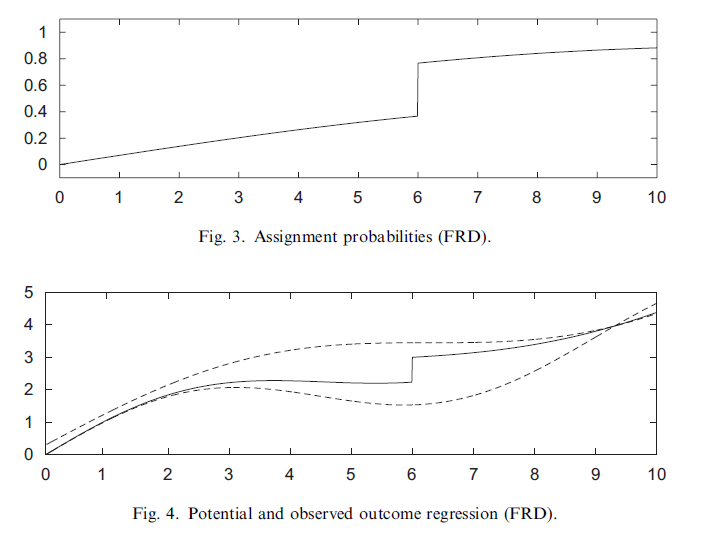
그림으로 쉽게 이해할 수 있다. SRD와 같이 0과 1이라는 값만 가지는 treatment 상황도 존재하지만, 대다수의 일반적인 상황에서는 특정 기준선을 전후로 조그마한 jump 정도만이 존재하는 경우가 많을 것이다.
예를 들어, 대학교에 입학하는 나이는 일반적으로 20살이라고 할 때, SRD의 경우에는 c=20을 기준으로 대학을 가고 안가고의 차이를 0과1로 나타낼 수 있지만, 현실에서는 후반기 입학생이 있을수도, 재수를 할수도, 조기입학을 할 수도 있기 때문에 FRD가 적합할 수도 있다는 것이다.
즉 discontinuity가 있다는 점에서 SRD와 공통점을 같지만, 그 차이가 0과 1일지, 혹은 서로 다른 두 값일지는 차이가 있을 것이다. 이로 인해, Fig 4를 보면 SRD의 그것(Fig 2)에 비해 점선에 붙어있는 실선이 아니라 그 사이의 값을 갖는 것을 알 수 있다. Prob가 0과 1이 아닌 어느 사이에 존재하기 때문.
SRD의 W의 간극이 1이라면 FRD는 0과 1 사이의 값을 갖기 때문에, FRD의 treatmente effect는 일종의 Wald estimator를 사용하여, 분모에 FRD 상의 W 간극을 보정해주는 과정을 취한다. 아래의 formular와 같다.
\[\tau_{FRD}=\frac{lim\;E[Y|c<-X]-lim\;E[Y|X->c]}{lim\;E[W|c<-X]-lim\;E[W|X->c]}\]External Validity
RD는 전체 population ($\forall x$)가 아닌 c와 그 근방의 극히 일부분만에 대해서 treatment effect를 확인하고 있기 때문에, 그 근방을 벗어난 다른 x들에 대해서는 inference를 할 수 없다는 단점이 있다. 즉 external validity는 낮다고 할 수 있다.
하지만 그 자체로 c라는 포인트에 대한 treatment effect를 estimate하는데 가장 객관적이고 논란이 덜 한 estimation으로 인정되고 있다. 즉 internal validity는 높다고 할 수 있다.
단 RD에서 중요한 것은 c를 비롯한 어떤 포인트 내의 sample (혹은 population)에서도 특별한 bias 없이 characteristic에 큰 차이가 없어야 한다는 것이다.
예를 들어 어떤 온라인 쇼핑몰에서 구매 총지출을 기준으로 회원 등급을 실버나 골드 등으로 나눈다고 할때, 사람들은 그 기준, treatment를 받기위한 조건 c를 알기 때문에 등급을 올리고자는 사람들은 지출을 일부러 더하는 등의 bias가 생길 수 있는 가능성이 충분하다 (그것도 c 포인트의 아주 근방에서만 발생할 것이다). 따라서 이럴 때엔 RD Design에 기반이 되는 비편향 조건에 문제가 생길 수 밖에 없을 것이다.
예시를 살펴보자!
Matsudaira. (2007)
Matsudaira. J.D. (2007) “Mandatory Summer School and Student Achievement” Journal of Econometrics 142:829-850.
미국에는 직전 봄학기 성적을 기준으로 여름 보충수업을 강제로 듣는 제도가 있는데, 이러한 기준을 전후로 발생하는 discontinuity를 통해 RD 를 활용한 연구를 진행하였다. DV는 곧, 여름 보충수업이 향후 학생 성적에 도움(효과)이 되는가 라는 RQ에 있어 학생의 성적이 DV가 될 것 이다.
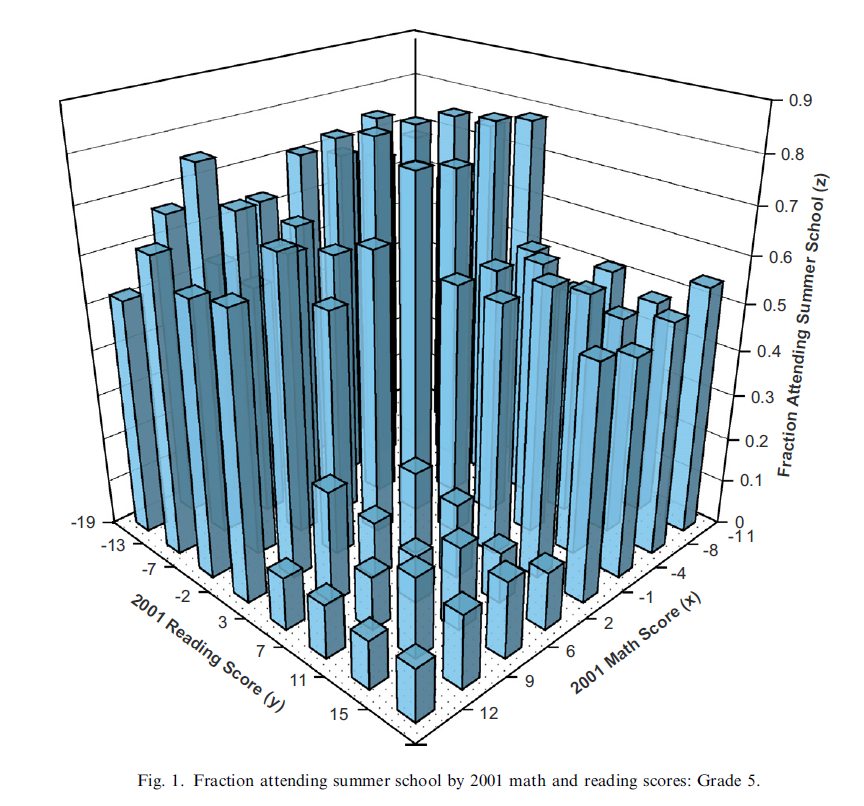
Matsudaira는 RD를 사용하였는데, 위의 Fig 1처럼 Reading 혹은 Math Score에 따라서 점수가 높은 학생들의 Summer School Attendance와 성적이 낮은 학생들 간의 Attendance 차이가 눈에 띄게 차이가나는 구간이 보일 것이다.
물론 성적이 높은 학생들도 자발적으로 Attending 할 수 있기 때문에 ???: 듣지마ㅏ!! 0과 1의 차이라기 보단 (rather than SRD), FRD가 더 적합한 연구 모델로서 사용될 것임을 우리는 알 수 있다.


댓글남기기