[Econometrics] 7-1. Instrumental Variables - Constant Effect

#IV #2SLS #ILS #Wald_estimator #weak_instrument

피곤하다

Instrumental Variables

Constant Effect

\[f_i(s)=\alpha+\rho s+\eta_i\]

본 Constant Effect 섹션에서는 treatment effect가 개인별에 차등없이 동일하게 적용되는 constant treatment effect 상황을 가정하고 진행하겠다.

흔히 IV를 공부할때 언급되는 케이스 중 하나인 학력과 연봉의 인과추론을 해보고자 한다.

우리가 알고 싶은 것은 학력이 연봉에 얼마나 영향을 주는지에 대한 treatment effect estimate $\rho$이다.

만약 s라는 schooling, 학력의 변수 말고도 능력이 연봉(unobserved, hence included at the $\eta$; OVB)에 유의한 상관관계가 존재한다면, OVB가 발생하며, s와 $\eta$ 사이의 correlation이 존재할 것이다. 그렇다면 $\eta$를 decompose 해보자.

\[\displaylines{\eta_i=A_i'\gamma+v_i\\ Cov(v_i, A_i)=0}\]

A는 능력에 관한 control variable이고, 남은 항 v는 곧 idiosyncratic error term이 될 것이다.

\[\displaylines{y_i=\alpha+\rho s+A_i'\gamma+v_i\\ \text{if we control } A_i\;\text{by CIA, we can identify }\rho}\]

우리는 앞선 장에서 배운 CIA를 통해 A를 통제해주면, v는 $\rho$와는 uncorrelated 되어있기 때문에 다시금 $\rho$를 제대로 구할 수 있다.

하지만 A를 통제하는 것은 매우 어렵다. 사람의 능력이라는 변수를 정량화 내지 측정이 가능한것일까?

Instrumental Variable

1. Instrument variable, z should be correlated with the causal variable of interest, s
2. z should be uncorrelated with potential outcomes
   1. $Cov(\eta, z)=0$

IV 변수 z를 통해 우리는 treatment effect를 y와 z, s와 z 간의 covariance ratio를 통해 구할 수 있다.

\[\displaylines{\text{For }\quad y_i=\alpha+\rho s+\eta_i \\\\ Cov(y,z)=Cov(\alpha+\rho s+\eta, z)\\ =0+\rho\, Cov(s,z) +0 \\ \text{Hence, }\; \rho=\frac{Cov(y,z)}{Cov(s,z)} \\\\ \rho=\frac{Cov(y,z)}{Cov(s,z)}\\ =\frac{Cov(y,z)/V(z)}{Cov(s,z)/V(z)} \equiv \frac{\text{reg y on z}}{\text{reg s on z}}\;\text{or}\;\frac{\text{Reduced Form}}{\text{1st stage}}}\]

Two-stage least squares (2SLS)

2SLS는 1) covariates를 추가하고, 2) 여러 개의 IV 변수들을 추가할 수 있다는 장점이 있다. 아래 수식에서 X는 covariates임을 기억하자.

\[\displaylines{y_i=\alpha' X_i+\rho s_i+\eta_i \\\\ \begin{cases} s_i=X_i'\pi_{10}+\pi_{11}z_i+\zeta_{1i} & \text{1st stage}\\\\ y_i=X_i'\pi_{20}+\pi_{21}z_i+\zeta_{2i} & \text{Reduced Form} \end{cases} \\\\ \text{Hence, }\; y_i=\alpha' X_i+\rho(X_i'\pi_{10}+\pi_{11}z_i+\zeta_{1i} )+\eta_i \\ =X_i'(\alpha+\rho \pi_{10})+\rho\pi_{11}z_i+[\rho\zeta_{1i}+\eta_i]\\ \equiv X_i'\pi_{20}+\pi_{21}z_i+\zeta_{2i} \\\\ \text{Thus, }\\ \begin{cases} \pi_{20}=\alpha+\rho \pi_{10}\\ \pi_{21}=\rho \pi_{11} & \rho=\frac{\pi_{21}}{\pi_{11}}=\frac{\text{Reduced Form}}{\text{1st stage}} \end{cases}}\]

우리는 위의 $\rho$를 두 식의 $\pi$에 대한 비율을 통해 구하는 과정을 Indirect Least Squares (ILS) 이라고 부른다. 두 개의 estimate를 통해 간접적으로 $\rho$를 구하기 때문이다.

ILS를 통해 estimator들을 통한 수식을 전개하면 아래와 같다.

\[\displaylines{s_i=X_i'\pi_{10}+\pi_{11}z_i+\zeta_{1i} \equiv \hat s_i+\zeta_{1i} \quad \text{by 1st stage}\\ \text{Then, }\; y_i=\alpha' X_i+\rho \hat s_i+[\eta_i+\rho\zeta_{1i}] \quad \text{hence it is reduced form (2nd stage)}}\]

지금까지 2SLS의 대략적인 전개를 살펴보았다. 우리는 manually 2SLS를 돌리지 않는데, 이는 두번에 거친 회귀식을 진행하는데에 있어 randomness 및 std. error를 제대로 구할 수 없기 때문이고, STATA 등의 통계 패키지 프로그램을 통해 구하는 것이 정확할 것이다.

Angrist, and Krueger (1991)

Angrist, and Krueger (1991). “Does Compulsory School Attendance Affect Schooling and Earnings?” Quarterly Journal of Economics, 106: pp. 979-1014.

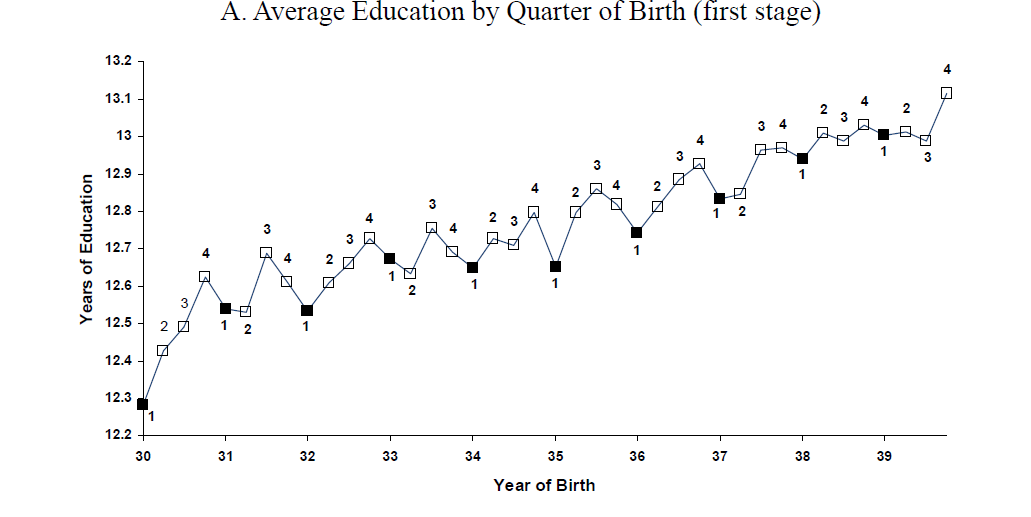
미국의 교육환경 및 의무교육제도 특성상, 같은 해라고 할지라도 4분기(QoB as IV)에 태어난 아이들이 조금 더 years of education(s), 교육연수해가 더 높은것을 알 수 있다.

즉, S와 Z의 관계를 확인하는 figure이다.

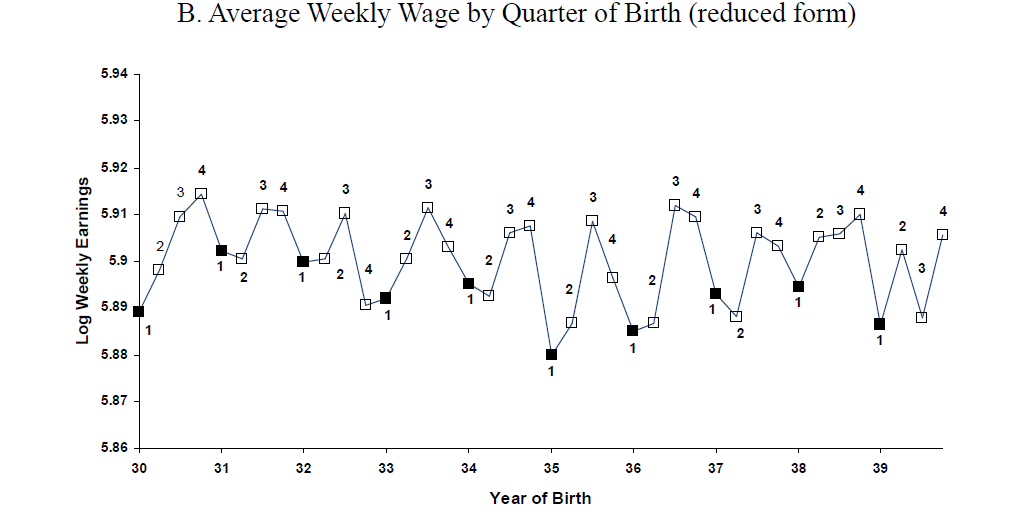
Y와 Z의 관계를 확인하는 두번째 figure이다.

따라서 우리는 IV인 QoB (이하 z)가 s와 y에 모두 correlation이 있는 것을 확인할 수 있다.

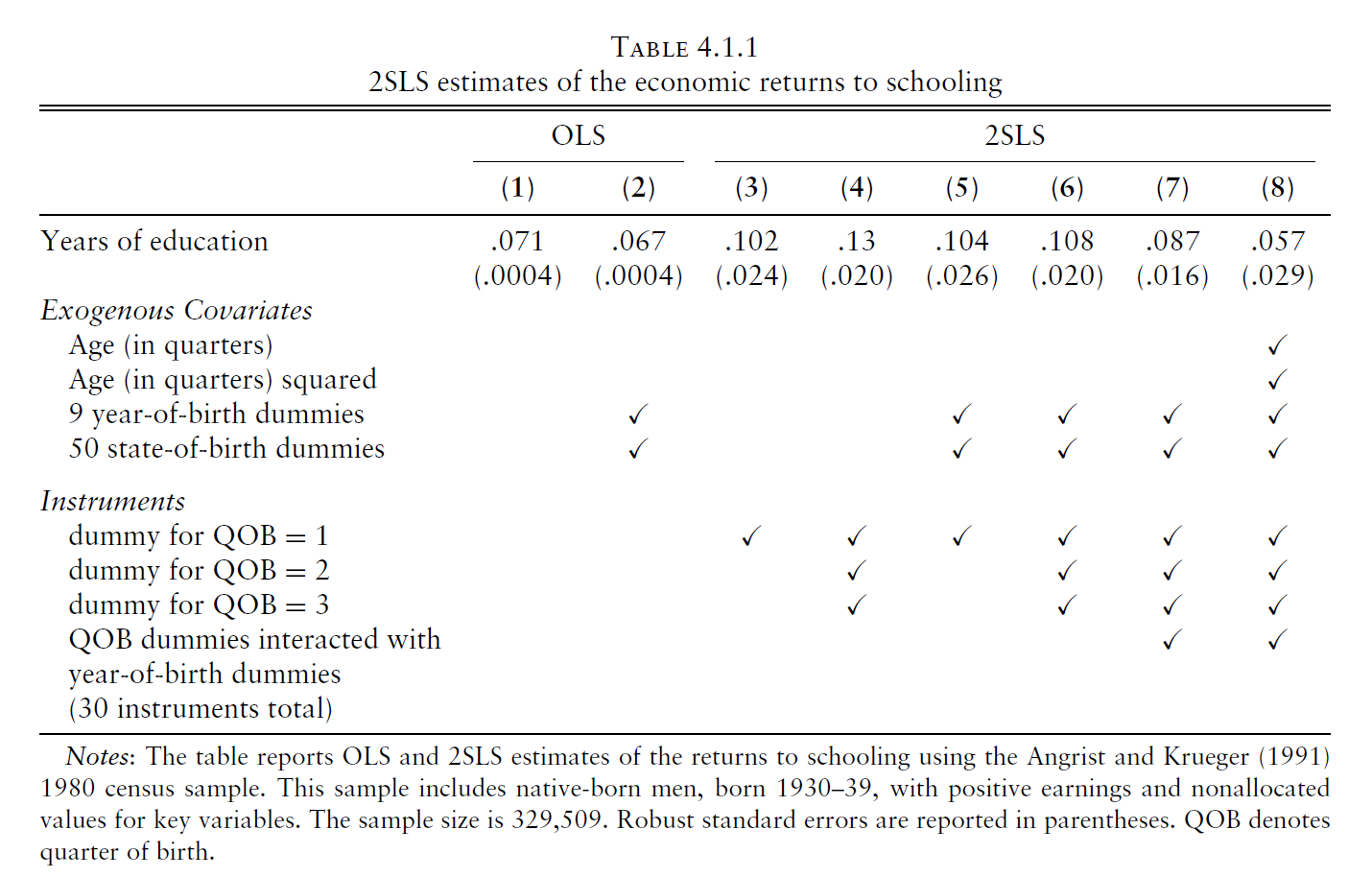
2SLS and ILS

IV 변수의 개수가 1개일 경우에는 2SLS와 ILS가 동일한 결과를 갖는다.

Multiple-Instrument 2SLS

\[\rho_{2SLS}=\phi\rho_1+(1-\phi)\rho_2\]

The Wald Estimator

z가 dummy variable일 땐 2sls estimator가 wald estimator로서 매우 심플한 공식을 가지게 된다.

Derivation 1)

\[\displaylines{Cov(y,z)=E(y,z)-E(y)E(z)\\ =\{E(y*1|z=1)p+E(y*0|z=0)(1-p)\} - \{E(y|z=1)p+E(y|z=0)(1-p)\}p \quad (\because E(z)=p)\\ =(1-p)p\{E(y|z=1)-E(y|z=0)\}\\ =Var(z)\{E(y|z=1)-E(y|z=0)\} \quad (\because Var(z)=p(1-p))\\ \\ \begin{cases} E(y|z=1)-E(y|z=0)=\frac{Cov(y,z)}{Var(z)}\\ E(D|z=1)-E(D|z=0)=\frac{Cov(D,z)}{Var(z)} \end{cases}\\\\ \text{Thus, } \quad \frac{E(y|z=1)-E(y|z=0)}{E(D|z=1)-E(D|z=0)}=\frac{Cov(y,z)}{Cov(D,z)}}\]

Derivation 2)

\[\displaylines{y=\alpha+\rho D+\eta\\ E(y|z)=\alpha+\rho E(D|z)+E(\eta|z) \\\\ E(y|z=1)=\alpha+\rho E(D|z=1)\\ E(y|z=0)=\alpha+\rho E(D|z=0) \\\\ E(y|z=1)-E(y|z=0)=\rho(E(D|z=1)-E(D|z=0)) }\]

Wald estimator는 매우 자주 사용되는 IV 활용 framework 중 하나라고 할 수 있다.

Weak Instrument

\[\displaylines{\begin{cases} Y=X\beta+\eta\\ X=Z\pi+\zeta \end{cases} \\\\ \text{The fitted value: }\; \hat X=Z\hat\pi=Z(Z'Z)^{-1}Z'X=P_Z X=Z\pi+P_Z \zeta \\ \hat\beta_{2SLS}=(\hat X'\hat X)^{-1}\hat X'Y\\ =(X'P_Z'P_Z X)^{-1}X'P_Z'Y\\ =(X'P_Z'P_Z X)^{-1}X'P_Z'X\beta+(X'P_Z'P_Z X)^{-1}X'P_Z'P_Z\eta\\ \\\\ \hat\beta_{2SLS}-\beta=(X'P_Z'P_Z X)^{-1}X'P_Z'P_Z\eta\\ =(X'P_Z X)^{-1}X'P_Z\eta=(X'P_Z X)^{-1}(\pi'Z'+\zeta')\eta\\ =(X'P_Z X)^{-1}\pi'Z'\eta+(X'P_Z X)^{-1}\zeta'\eta \\\\ E[\hat\beta_{2SLS}-\beta]=(X'P_Z X)^{-1}\zeta'\eta \quad (\because E(Z'\eta)=0) }\]

1st stage의 error term, $\zeta$와 $\eta$가 correlation이 있고, Z의 설명력이 부족해 $Z\pi$ 항의 크기가 줄고 상대적으로 $\zeta$의 항 크기가 커지면, bias가 증가할 것이다.

\[\displaylines{\text{for} \quad E[X'P_Z X]^{-1}\\\\ E[X'P_Z X]^{-1}=(E[(\pi'Z'+\zeta')P_Z(Z\pi+\zeta)])^{-1}\newline =(E[(\pi'Z'+\zeta'P_Z)(Z\pi+\zeta)])^{-1}\newline =(E[\pi'Z'Z\pi]+E[\pi'Z'\zeta]+E[\zeta'P_Z Z\pi]+E[\zeta'P_Z\zeta])^{-1}\newline =(E[\pi'Z'Z\pi]+E[\zeta'P_Z\zeta])^{-1}}\] \[\displaylines{\text{for} \quad E[\zeta'P_Z\zeta] \\\\ E[\zeta'P_Z\zeta]=\sigma_\zeta^2 tr(P_Z) \equiv \sigma_\zeta^2 Q}\] \[\displaylines{\text{for} \quad E[\zeta P_Z \eta] \\\\ E[\zeta P_Z \eta]=\sigma_{\eta\zeta} tr(P_Z) \equiv \sigma_{\eta\zeta} Q}\] \[\displaylines{\text{Thus, for} \quad E[\hat\beta_{2SLS}-\beta]\\\\ E[\hat\beta_{2SLS}-\beta]=E[X'P_Z X]^{-1} E[\zeta P_Z \eta]\newline =(E[\pi'Z'Z\pi]+E[\eta'P_Z\eta])^{-1} E[\zeta P_Z \eta]\newline =(E[\pi'Z'Z\pi]+\sigma_\zeta^2 Q)^{-1} * \sigma_{\eta\zeta} Q\newline =(\frac{E[\pi'Z'Z\pi]}{\sigma_\zeta^2 Q}+1)^{-1} * \frac{\sigma_{\eta\zeta} Q\newline}{\sigma_\zeta^2 Q}\newline =\frac{\sigma_{\eta\zeta}}{\sigma_\zeta^2}(\frac{E[\pi'Z'Z\pi]/Q}{\sigma_\zeta^2}+1)^{-1}\\ \equiv \frac{\sigma_{\eta\zeta}}{\sigma_\zeta^2}\frac{1}{(F+1)} }\]

우리는 F를 위의 식에 참고하여 Q에 반비례하는 항으로 정의된것을 확인할 수 있는데, 곧 의미없는 도구변수의 추가가 Q의 증가로 인한 F 값의 감소로 $\pi$가 감소하고 곧, 2SLS의 bias가 OLS의 그것과 다를게 없다는 것을 보여주고 있다.

결국 문제는 $x$가 아닌 $\hat x$를 사용했기 때문에 나타난 문제이고, Just-identified 2SLS는 unbiased 하다고 할 수 있다.

물론 어떤 경우에도, Reduced Form은 기본적인 가정 y와 z의 uncorrelation에 따라 bias가 없다고 한다.